How Do You Draw A Graph Of A Function?

Related Pages
Reciprocal Of A Function
Graphs Of Functions

How To Graph Reciprocal Functions?

There are several forms of reciprocal functions. One of them has the form y = , where k is a real number and x ≠ 0.

What Are The Characteristics Of The Graph Of A Reciprocal Function?

The graph of y = gets closer to the ten-axis as the value of 10 increases, simply information technology never meets the x-axis. This is called the horizontal asymptote of the graph.

Each piece of the graph besides gets closer to the y-centrality as 10 gets closer to 0 but it never meets the y-axis considering there is no value for y when ten = 0. This is called the vertical asymptote of the graph.

This blazon of curve is called a rectangular hyperbola.

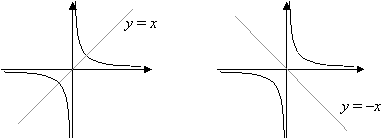
Note that this type of curve, the graphs of y = where 1000 is a real number and ten ≠ 0, has two lines of symmetry: y = x and y = x.

How To Graph Reciprocal Functions By Plotting Points?

Example:
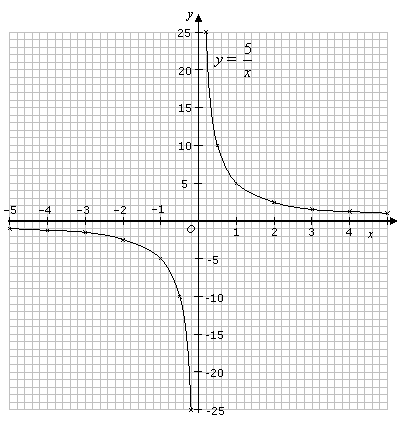
Draw the graph of y = for values between 4 and 4, except for x = 0.

Solution:

x	0.2	0.v	one	2	iii	4	5
y	25	10	5	2.5		1.25	ane

x	0.2	0.5	1	2	three	4	v
y	25	x	5	2.v		ane.25	ane

The curve consists of 2 divide pieces, only they should be regarded as ane graph.

How To Utilise Transformation To Graph Reciprocal Functions?

Introduction to reciprocal functions, identifying asymptotes and graphs of reciprocal functions, stretching, shrinking, and translating reciprocal functions, and graphing reciprocal functions.

y = one/x and y = a/(x − h) + one thousand.
Stretch when a > 1 and shrink when 0 < a < 1.
Graphs for positive and negative a values.
h translates horizontally and k translates vertically.

Examples:

1. Compare the graphs y = 1/10, y = 5/x and y = 1/(5x)
2. Compare the graphs y = ane/ten and y = -1/x
3. Compare the graphs y = 1/x, y = one/(x - 4) and y = 1/x - 4
4. Graph y = 2/(ten - 4) + 1000

• Show Video Lesson

Depict The Characteristics Of The Reciprocal Function f(x) = 1/x

Explain the domain, range, vertical and horizontal asymptotes.

• Prove Video Lesson

Transformation Of Reciprocal Functions

How to use transformation to graph reciprocal functions?

\(f(ten) = \frac{a}{{x - h}} + k\)

h is the horizontal translation
if h is positive, shifts left
if h is negative, shifts right
h also shifts the vertical asymptote

k is the vertical translation
if k is positive, shifts upwards
if grand is negative, shifts downwardly
k also shifts the horizontal asymptote

a is orientation and shape
if a is negative, reflection across x-axis
if a > i, stretched vertically
if 0 < a < 1, compressed vertically

Example:
Graph, then state the domain, range and asymptotes

1. \(f(x) = \frac{2}{{x}} + 3\)
   
2. \(f(ten) = \frac{3}{{10 - 2}}\)
   
3. \(f(x) = \frac{4}{{ten + 3}} - 5\)
   
4. \(f(x) = \frac{4}{{x^2}} - 4\)
   
5. \(f(x) = 6 - \frac{2}{{(10 - 3)^2}}\)

• Show Video Lesson

How To Graph A Reciprocal Role With A Horizontal Translation?

Sketch the Reciprocal Function using Transformations

Case:
Graph y = 1/(x - 3).

• Prove Video Lesson

Graphing Transformations Of Reciprocal Function

Example:
Given the function \(y = \frac{{ - two}}{{3(x - 4)}} + 1\)
a) Determine the parent role
b) Land the argument
c) Rearrange the argument if necessary to determine and the values of k and d
d) Rearrange the function equation if necessary to determine the values of a and c
eastward) State the transformations (in an appropriate order) that are performed on the graph of the parent role to obtain the graph of the function given.

Method ane:
f) Graph each transformation in the advisable order given in function e), and testify the graph of the given function in a distinctive colour.

Method 2:
yard) Use the table method to determine coordinate of the office given, the graph.

Method 3:
h) Apply the transformation formula to determine coordinates of the office given, then graph.

• Testify Video Lesson

How To Graph Reciprocal Functions When Given The Equation?

How to graph functions that are ane/ten and variations of that.

Find asymptotes, intercepts, and employ a couple test values.

1. To get the vertical asymptote, set denominator = 0
2. To get the horizontal asymptote, imagine x getting really big
3. To get the y-intercept, ready x = 0
4. To go the ten-intercept, set y = 0
5. Do test values on either side of the vertical asymptote

Case:
Graph m(x) = \(y = \frac{{ - 17}}{{18 - 8x}} - iv\).

• Show Video Lesson

How To Find The Equation Of A Reciprocal Role When Given Its Graph?

This video shows how to get the equation of a reciprocal office from its graph.

1. Notice the vertical asymptote. This is the root of the denominator.
2. Find the horizontal asymptote. This is added/subtracted from your fraction.
3. Notice a signal on the curve, and plug into the equation. Solve for numerator.

• Show Video Lesson

Another form of reciprocal functions is y = , where g is a existent number and x ≠ 0.

Example:
Draw the graph of y = for 4 ≤ x ≤iv and x ≠ 0.

Solution:

10	4	3	ii	ane	0.8	0.8	ane	ii	3	iv
y	0.19	0.33	0.75	three	iv.69	iv.69	3	0.75	0.33	0.19

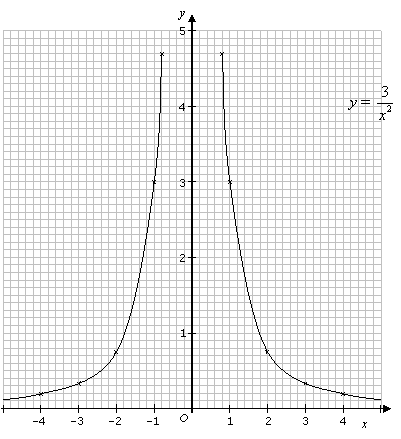
Notice that graphs of y = , where g is a existent number and x ≠ 0, has an centrality of symmetry on the y-axis (i.e. x = 0)

Attempt the free Mathway computer and problem solver below to practice diverse math topics. Effort the given examples, or blazon in your ain problem and check your answer with the step-by-stride explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback folio.

Source: https://www.onlinemathlearning.com/reciprocal-function.html

Posted by: hammerstherong1944.blogspot.com

Share this post